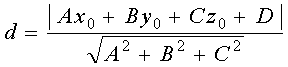§7.7
平面及其方程
一 平面的点法式方程
若一非零向量垂直于一平面,则称此向量是该平面的法线向量。
显然,平面上的任一向量均与平面的法线向量垂直。由于过空间一点可以作而且只能作一个平面垂直于一已知直线。
因此,当平面![]() 上一点
上一点![]() 和它的一个法线向量
和它的一个法线向量 ![]() 给定之后,平面的位置就确定下来了。
给定之后,平面的位置就确定下来了。
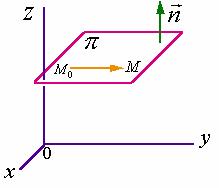
下面,我们来建立这种平面方程。
设![]() 是
是![]() 上的任一点,那未,
上的任一点,那未,![]() ,即
,即 ![]()
而
![]()
若设
![]() ,故
,故
![]() (1)
(1)
这表明:平面![]() 上任一点
上任一点![]() 的坐标满足方程(1)。
的坐标满足方程(1)。
反过来,若点![]() 不在平面
不在平面![]() 上,向量
上,向量![]() 就不垂直于
就不垂直于![]() ,从而
,从而 ![]() ,即
,即 ![]()
亦即:不在平面![]() 上的点
上的点![]() 的坐标不适合方程(1)。
的坐标不适合方程(1)。
故,方程(1)就是平面![]() 的方程,而平面
的方程,而平面![]() 便是方程(1)的图形。
便是方程(1)的图形。
因为方程(1)是由平面![]() 上一点
上一点![]() 及它的一个法线向量
及它的一个法线向量![]() 唯一确定的,因此,方程(1)也称之为平面的点法式方程。
唯一确定的,因此,方程(1)也称之为平面的点法式方程。
二
平面的一般方程
注意到,方程(1)是![]() 的一次方程,我们可断言:任一平面都可以用三元一次方程来表示。
的一次方程,我们可断言:任一平面都可以用三元一次方程来表示。
这是因为任一平面都可以由它的法线向量与它上面的一点唯一决定,而平面的点法式方程本身就是三元一次方程。
反过来,若有三元一次方程
![]() (2)
(2)
任取满足该方程的一组数![]() ,即
,即
![]()
两式相减得
![]() (3)
(3)
显然,方程(3)是过点![]() 且以
且以![]() 为法线向量的平面方程,而方程(2)与方程(3)是同解的,由此可知, 三元一次方程(2)所代表的图形是平面。
为法线向量的平面方程,而方程(2)与方程(3)是同解的,由此可知, 三元一次方程(2)所代表的图形是平面。
方程(2)称为平面的一般方程 ,该平面的法向量是由![]() 的系数所作成的向量
的系数所作成的向量![]() 。
。
对于一些特殊的三元一次方程,它们所代表的平面具有一些特殊性。
1、当![]() 时,(2)式成为
时,(2)式成为![]() ,它表示一个通过原点的平面,因为
,它表示一个通过原点的平面,因为![]() 的坐标显然适合该方程。
的坐标显然适合该方程。
2、当![]() 时,(2)式成为
时,(2)式成为![]() ,法线向量为
,法线向量为![]() ,因
,因 ![]() ,(
,(![]() ),故
),故![]() ,
,![]()
![]() ,从而平面
,从而平面 ![]() 平行于
平行于![]() 轴。
轴。
类似地,方程![]() 表示平行于
表示平行于![]() 轴的平面;方程
轴的平面;方程 ![]() 表示平行于
表示平行于![]() 轴的平面。
轴的平面。
3、当![]() 时,(2)式成为
时,(2)式成为![]() 或
或![]() ,法线向量
,法线向量![]() 同时垂直于
同时垂直于![]() 轴,
轴,![]() 轴,故方程表示过点
轴,故方程表示过点![]() ,且平行于
,且平行于![]() 面的平面。
面的平面。
类似地,方程![]() 表示过点
表示过点![]() 且平行于
且平行于![]() 面的平面;方程
面的平面;方程![]() 表示过点
表示过点![]() 且平行于
且平行于![]() 面的平面。
面的平面。
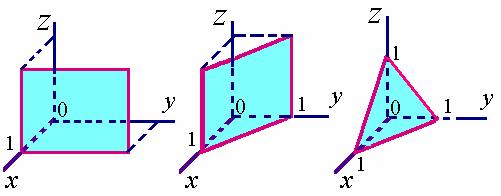
【例一】画出下列平面的图形
(1)、![]() (2)、
(2)、![]() (3)、
(3)、![]()
【例二】求通过![]() 轴和点
轴和点![]() 的平面方程。
的平面方程。
解:平面过![]() 轴,则该平面的法线向量垂直于
轴,则该平面的法线向量垂直于![]() 轴,且平面过原点,
轴,且平面过原点,
故设该平面的方程为 ![]()
由平面过点![]() ,有
,有 ![]()
![]()
将此式代入所设方程有
![]()
约去非零因子![]() ,得平面方程
,得平面方程
![]()
注明:为什么![]() 呢?
呢?
若![]() ,那么该平面的法线向量
,那么该平面的法线向量![]() ,这与平面法线向量必须为非零向量的规定相矛盾。
,这与平面法线向量必须为非零向量的规定相矛盾。
【例三】设一平面与![]() 轴,
轴,![]() 轴,
轴,![]() 轴分别交于三点
轴分别交于三点 ![]() ,
,![]() ,
,![]() 求此平面的方程(其中:
求此平面的方程(其中:![]() )。
)。
解:设所求的平面方程为
![]() ,
,
将三点的坐标分别代入得

及 ![]()
代入所设方程有
![]()
两边同除以![]() 有
有
![]() (4)
(4)
方程(4)称之为平面的截距式方程,而![]() 依次称作平面在
依次称作平面在![]() 轴上的截距。
轴上的截距。
三
两平面间的夹角
两平面的法线向量的夹角称作两平面间的夹角。
下面,我们阐述一下用两平面间法线向量的夹角来定义两平面间夹角的合理性。
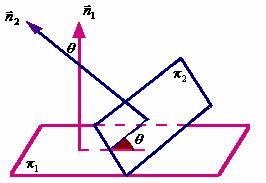
如图所示,设想平面![]() 与平面
与平面![]() 重合在一起的,于是它们的法线向量应平行,即
重合在一起的,于是它们的法线向量应平行,即 ![]() 。将平面
。将平面![]() 的一侧向上提起,与
的一侧向上提起,与![]() 之间产生倾角
之间产生倾角![]() 。与此同时,
。与此同时,![]() 的法线向量
的法线向量![]() 发生转动,与平面
发生转动,与平面![]() 的法线向量
的法线向量![]() 产生的角度
产生的角度![]() 。
。
下面,我们导出计算两平面夹角![]() 的公式
的公式
设有平面![]()
![]()
和平面![]()
![]()
则![]() 与
与![]() 的法线向量分别为
的法线向量分别为 ![]() ,
,
两向量间夹角的余弦为
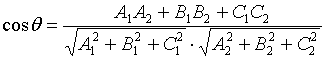 (5)
(5)
由(5)式,立刻可给出如下结论:
1、![]()
2、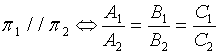
【例四】一平面过两点 ![]() 和
和 ![]() 且垂直于平面
且垂直于平面
![]() ,求它的方程。
,求它的方程。
解:设所求平面的法线向量为
![]()
显然,
![]() 在所求平面上,
在所求平面上,
故
![]() ,
, ![]() ,即
,即
![]()
又![]() 垂直于平面
垂直于平面![]() 的法线向量
的法线向量![]() ,故有
,故有
![]()
解方程组
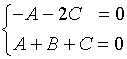 得:
得: 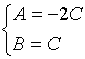
据点法式方程有
![]()
约去非零因子
![]() 得
得
![]()
故所求方程为 ![]()
【例五】 设![]() 是平面
是平面![]() :
: ![]() 外一点, 求点
外一点, 求点![]() 到平面
到平面![]() 的距离。
的距离。
解:在平面![]() 任取一点
任取一点![]() ,作平面
,作平面![]() 的法线向量
的法线向量![]() ,
,
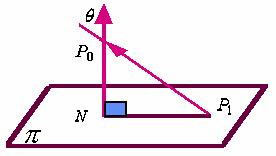
如图,作向量![]() , 记
, 记![]() 与
与![]() 之间的夹角为
之间的夹角为![]() ,
,
![]() 到平面
到平面![]() 的距离
的距离 ![]()
考虑到夹角![]() 可能是钝角,取距离为
可能是钝角,取距离为 ![]()
![]()
![]()
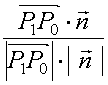
![]()
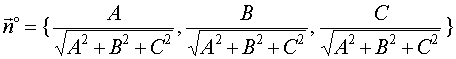
![]()
则
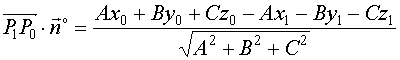
而
![]()
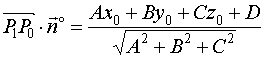
故